


Ondanks deze uitdagingen is het schrijven van cijfers makkelijker te leren dan het schrijven van letters. De route die de pen moet volgen is bij cijfers makkelijker te doorzien dan bij letters. Er is slechts één cijfer waar de pen overlappende streken maakt, en dat is de 9. Er hoeven geen verbindingen tussen de cijfers aangeleerd te worden. Een slordig geschreven l lijkt precies een e, maar er zijn slechts weinig cijferparen die met elkaar verward kunnen worden.
Als een leerling elke letter afzonderlijk leesbaar kan schrijven, betekent het niet dat hij ook woorden leesbaar kan schrijven. Het verbinden van letters aan elkaar (of bij onverbonden schrift: het plaatsen van letters op een kleine maar gelijkmatige afstand van elkaar) is een vaardigheid die aangeleerd moet worden. Voor cijfers geldt hezelfde. Een leerling die in staat is tot het schrijven van leesbare cijfers, is nog niet automatisch in staat tot het schrijven van leesbare getallen. Bij het schrijven van letters leren we leerlingen tussen de lijntjes schrijven voordat we ze letters aan elkaar laten verbinden. De goede schrijfmethodes gebruiken een volledige liniatuur (grondlijn, romplijn, luslijnen) al bij de eerste kennismaking met een nieuwe letter. Bij cijfers moeten we precies hetzelfde doen.
De beste manier om te zorgen dat een leerling de stap van leesbare losse cijfers naar leesbare getallen kan maken, is door de leerling vanaf het begin de cijfers in hokjes (ruitjes) te laten schrijven.
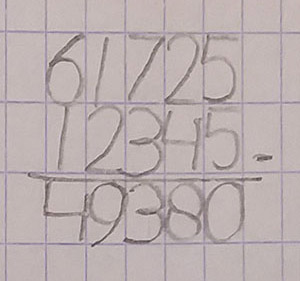
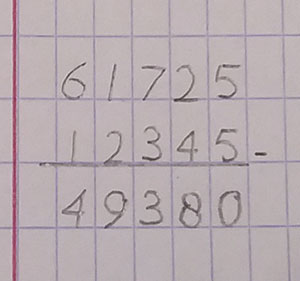
In Schriftvaardig (Scholten & Hamerling)Schriftvaardig is verkrijgbaar via Webedu.nl. De auteurs zijn tevens oprichters van de Stichting Schriftontwikkeling. Lees hier meer over in hoeverre ideeën op syboor.eu afkomstig zijn van de Stichting Schriftontwikkeling. krijgt de student drie regels (criteria) voor het schrijven van de cijfers:

In sommige schrijfmethodes worden de cijfers uitgevuld - dwz tegen de zijkanten en/of de bovenkant van het hokje - geschreven. De leerling leert geen afstand houden, en wordt daardoor helaas niet goed voorbereid op het schrijven van getallen van meerdere cijfers.
Over het algemeen geldt: hoe meer kaders de beginner krijgt, hoe beter. Het schrijven van cijfers tussen twee lijnen met startpunten (zoals in de Junior Einstein materialen) is al veel beter dan alleen maar een grondlijn. Maar vanwege de uitdagingen met de horizontale positionering van cijfers is het schrijven in hokjes het beste.


Op internet zijn ook veel materialen waarbij een cijfer helemaal middenin een hokje geschreven wordt, dus zwevend boven de grondlijn. Dit is te vrijblijvend. Juist door te proberen precies op de grondlijn uit te komen - en te zien of dit gelukt is - krijgt de leerling controle over de hoogte van zijn cijfers.
Op deze site worden cijferkaarten en ruitjesliniaturen aangeboden met rechthoekige hokjes. Je kunt kiezen tussen hokjes met de 2:1 verhouding zoals gebruikt in de methode Schrift, of hokjes met de 9:5 verhouding die in methodeonafhankelijk rekenschriften veel gebruikt wordt.
Op de middelbare school wordt bij wiskunde gebruik gemaakt van vierkante hokjes. Vierkante hokjes zijn beter geschikt voor meetkunde dan de rechthoekige hokjes van de basisschool. Op de middelbare school hoeft de leerling echter niet meer te cijferen (de rekenmachine wordt gebruikt) en heeft de leerling bovendien goed inzicht in de getalstructuur; de horizontale positie van de cijfers in een getal is daardoor minder belangrijk. Voor kinderen die nog bezig zijn met leren schrijven en leren rekenen zijn rechthoekige hokjes het meest geschikt. Rechthoekige hokjes zorgen ervoor dat je verticaal meer afstand houdt dan horizontaal, en dat is precies wat nodig is om zichtbaar te maken welke cijfers tot hetzelfde getal behoren, want getallen worden horizontaal geschreven.
Op de onderstaande cijferkaarten is de route van de cijfers aangegeven dmv stoplichtmarkering: eerst groen, dan blauw, dan rood (geen oranje, omdat ik geen oranje pennen heb die goed zichtbaar zijn op een witte achtergrond). Voor eigen gebruik kun je het beste een outlineversie van de cijferkaart afdrukken en zelf de markeringen aanbrengen.
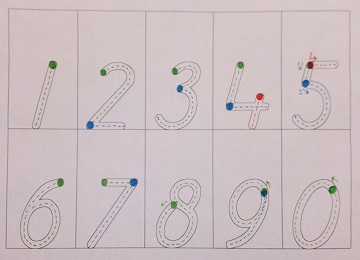

Met de route van de cijfers worden de bewegingen benadrukt die bij het schrijven van de letters ook veel gebruikt worden, en die bij de juiste schuine stand van papier en arm makkelijk te maken zijn: van boven naar beneden, en tegen de klok in. Een “verkeerde” route is echter bij de cijfers niet zo'n groot probleem als bij de letters. Er is geen sprake van een verbinding tussen tekens die verkeerd gaat als een leerling het eerste teken op de verkeerde plaats afrondt. Als een leerling inconsequent is met de route is het goed dit te corrigeren: een leerling die steeds hetzelfde proces volgt, zal sneller controle krijgen over het resultaat. Maar een consequent “verkeerd” ingeslepen route hoeft niet verbeterd te worden als de vorm van het cijfer verder goed is.
Voor het aanleren van de route raad ik aan om net als bij de letters een “cijferfilm” te schrijven, alleen dan mbv lege hokjes ipv lege lijntjes. Het beste is als de leerlingen zelf de stoplichtmarkeringen aanbrengen als verwerking na de instructie. Alleen als leerlingen zelf een stoplichtcijfer gemaakt hebben, kun je er zeker van zijn dat ze de informatie in het stoplichtcijfer ook kunnen “aflezen”.
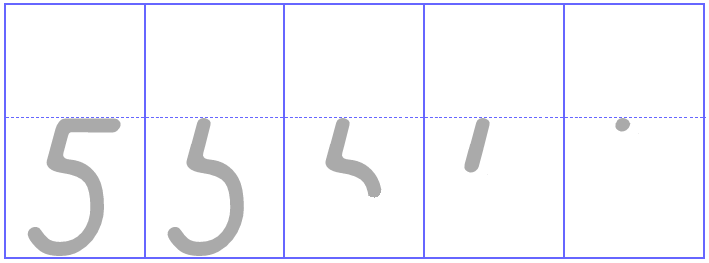
De cijferkaarten op deze website zijn allemaal beschikbaar in outlineversie, zodat je je eigen markering in de cijfers kunt aanbrengen. Dat kan een stoplichtmarkering zijn, maar ook andere markeringen (bijv. genummerde pijlen) zijn mogelijk.
Voor feedback op en zelfevaluatie van het schrijfwerk kunnen de onderstaande succescriteria met de leerling gedeeld worden.
Zo schrijf ik makkelijk leesbare cijfers:
Letters worden vaak geschreven met een hellingshoek van 15°. De meeste schrijfmethodes schrijven de cijfers ook hellend. Het is echter niet noodzakelijk om letters en cijfers met dezelfde hellingshoek te schrijven. Het schrijven in hokjes - en dan vooral het horizontaal positioneren en het resultaat beoordelen - gaat makkelijker als er rechtop geschreven wordt. Verwarring tussen de 1 en de 7 is minder waarschijnlijk wanneer er rechtop geschreven wordt. Een nadeel van rechtop schrijven is dat sommige leerkrachten het lelijk vinden als rechtopstaande cijfers in een hellend geschreven zin gebruikt worden. Overigens, in de wiskunde worden hellend en rechtopstaand schrift vaak door elkaar gebruikt. Letters (de variabele x, de zwaartekrachtconstante g) worden schuin geschreven zodat ze makkelijker te onderscheiden zijn van het (rechtop geschreven) vermenigvuldigingsteken × of het cijfer 9.
Bij de materialen op deze site kun je kiezen tussen hellende cijfers of rechtop geschreven cijfers.
Het cijfer 1 kan met ophaal geschreven worden of zonder. In tekstverband is bij de 1 met ophaal duidelijker dat het om een cijfer gaat; in getalverband (bij cijferend rekenen etc.) is een 1 zonder ophaal voldoende duidelijk. De 1 met ophaal kan verward worden met de 7, vooral bij hellend schrift. Als je een 1 met ophaal schrijft, schrijf de 7 dan met een dwarsstreepje.
De cijfers 2 en 7 worden soms geschreven met een golfje onder (2) of boven (7).
Op deze website zijn cijfervarianten met golfjes alleen beschikbaar in hellende vorm, en alleen in combinatie met het dwarsstreepje bij de 7.
Het cijfer 4 kan ‘open’ geschreven worden, met twee evenwijdige neerhalen. Of het kan gesloten geschreven worden, waarbij de twee neerhalen vanuit één punt vertrekken. Of het cijfer kan ‘puntig’ en ‘open’ tegelijk zijn: door een stukje weg te laten bij de tweede (korte) neerhaal.
Al deze drie varianen zijn op deze website beschikbaar als losse outlinecijfers, zowel hellend als rechtop. Op de cijferkaarten worden twee varianten aangeboden.
Het cijfer 8 kan geschreven worden zodat het begint en eindigt op dezelfde plek, die daardoor een kruispunt wordt, en waarbij de twee cirkels elkaar uitsluitend op het kruispunt aanraken. Het cijfer 8 kan ook geschreven worden met het begin- en eindpunt versprongen ten opzichte van elkaar. Het verspringen maakt de route iets makkelijker te doorzien, en maakt de bovenste cirkel wat groter (waardoor er minder risico is op het ‘dichtlopen’ van de cirkel bij een bot potlood).
Beide varianten van het cijfer 8 zijn in de materialen op deze website beschikbaar.
Uithangende cijfers worden zelden nog gebruikt. Voor het rekenen in een rekenschrift zijn ze niet geschikt. Leerlingen moeten sowieso tabelcijfers leren schrijven, en het is het beste om dat eerst te doen.
Het font “Schoolschrift” beschikt over uithangende cijfers. Deze worden niet verder doorontwikkeld: dat wil zeggen dat er geen varianten beschikbaar zijn en geen rechtopstaande versie. In de “Schoolschrijver”-app op deze site kunnen ze gekozen worden. In andere materialen en gereedschappen op deze site zul je ze niet terugvinden.
De tabelcijfers in het font “Schoolschrift” zijn vrij klein ten opzichte van de letters. Voor gemengde oefeningen met cijfers en tekst is “Schoolschrift” daarom niet zo geschikt. Materialen met een mengsel van cijfers en tekst zul je daarom niet vinden op deze website, hoewel het met sommige gereedschappen misschien wel mogelijk is ze te maken.
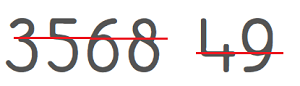
Bij de cijfers 3, 5, 6, 8 is de 'onderste' helft groter dan de bovenste. Je moet klein beginnen zodat je goed uitkomt op de grondlijn. Bij 4 en 9 is juist de bovenste helft groter dan de onderste.
Op deze site zijn de interne verticale verhoudingen van de cijfers 3, 5, 6 en 8 hetzelfde. Je kunt een hulplijn trekken om leerlingen te helpen die moeite hebben met deze verhoudingen. Ook de verhoudingen van de cijfers 4 en 9 zijn hetzelfde (maar anders dan bij 3, 5, 6 en 8).
Cijfers hebben meerdere varianten qua vorm, die allemaal goed leesbaar kunnen zijn. Voor de leesbaarheid van getallen en van rekenwerk is het belangrijk om cijfers vanaf het begin te oefenen in hokjes, waarbij de cijfers de zijkanten en bovenkant van de hokjes niet mogen raken.